LeetCode 239. 滑动窗口最大值 题解理解,理解空间换时间、区间最值问题解。
239. 滑动窗口最大值#
https://leetcode.cn/problems/sliding-window-maximum/
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
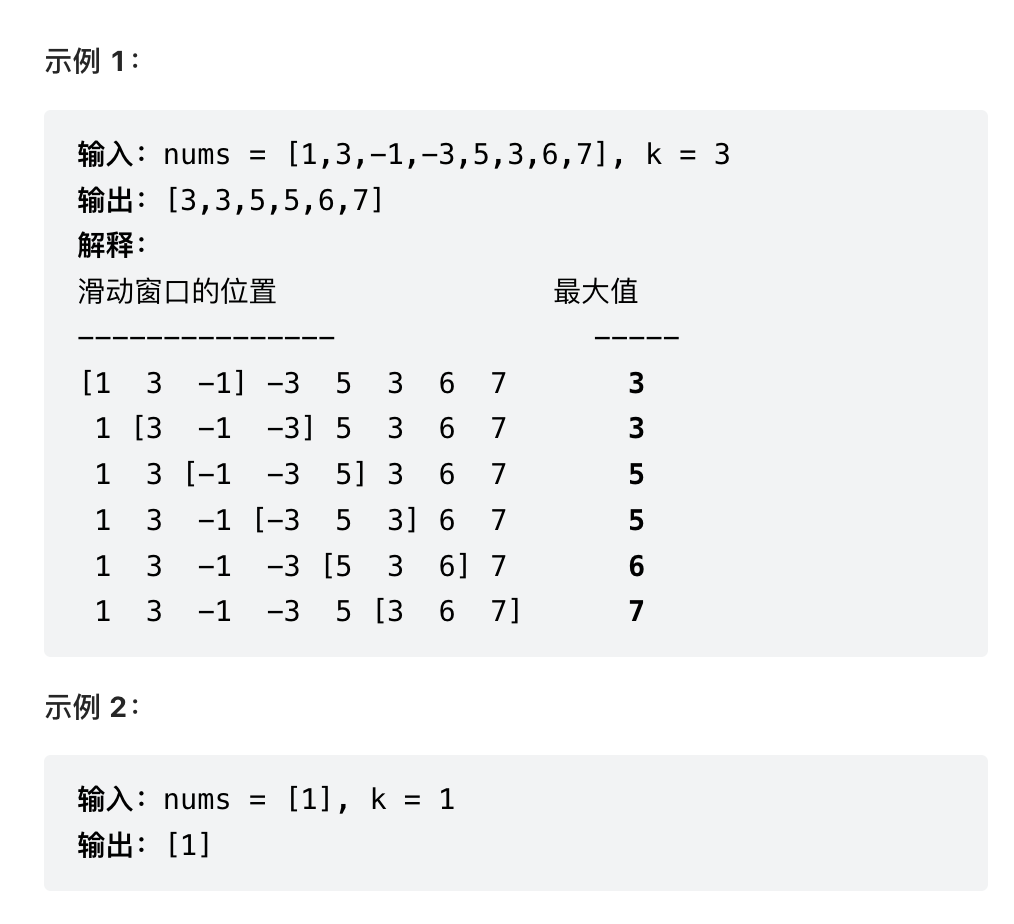
首先写一个暴力解法,典型的O(n^2)复杂度,当然就超时了。于是我们考虑,是不是可以空间换时间?
暴力解#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
/**
* 暴力解法最直观,每次分组k个,我们遍历k个元素选出最大值
* 优点:直观
* 缺点:时间复杂度过高 O(n^2)
*/
public int[] maxSlidingWindowBF(int[] nums, int k) {
int[] ans = new int[nums.length - k + 1];
for (int i = 0; i < ans.length; i++) {
int max = nums[i];
for (int j = 1; j < k; j++) {
max = Math.max(max, nums[i + j]);
}
ans[i] = max;
}
return ans;
}
|
使用最大堆维护当前需统计的数据#
最大堆解法,使用最大堆维护当前需统计的数据,当前最大值只要还在k个一组下标范围内就不出堆,否则将非法最大值移出堆。
堆顶即为一组中的最大值,O(1)即可获取最大值。
维护统计数据时间复杂度:O(nlogn),最差情况下碰到递增序列,堆维护了n容量的数据。
用例分析:
- 递增序列:最大值一直入堆,旧数据不管
- 递减序列:堆最大元素每次均淘汰刚出界的前最大值,更新当前组最大值
- 等值序列:最大值一直入堆,旧数据由于下标出界出堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
/**
* 最大堆解法,使用最大堆维护当前需统计的数据,当前最大值只要还在k个一组下标范围内就不出堆,否则将非法最大值移出堆
* <p>
* 堆顶即为一组中的最大值,O(1)即可获取最大值
* 维护统计数据时间复杂度:O(n*logn),最差情况下碰到递增序列,堆维护了n容量的数据
* <p>
* 用例分析:
* - 递增序列:最大值一直入堆,旧数据不管
* - 递减序列:堆最大元素每次均淘汰刚出界的前最大值,更新当前组最大值
* - 等值序列:最大值一直入堆,旧数据由于下标出界出堆
*/
// @formatter:off
public int[] maxSlidingWindowWithMaxHeap(int[] nums, int k) {
int n = nums.length;
// 最大堆:存储 nums[i],i
PriorityQueue<int[]> maxHeap = new PriorityQueue<>(
// 先以 nums[i]倒序,相等,再以 i下标倒序
(pair1, pair2) -> pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1]
);
// 先将第一组k个数据入堆
for (int i = 0; i < k; ++i) {
maxHeap.offer(new int[]{nums[i], i});
}
int[] ans = new int[n - k + 1];
ans[0] = maxHeap.peek()[0];
// 遍历后续数据
for (int i = k; i < n; ++i) {
// 先入堆下一组的新数据
maxHeap.offer(new int[]{nums[i], i});
// 如果此时最大堆堆顶下标超出了组边界,出堆
while (maxHeap.peek()[1] <= i - k) {
maxHeap.poll();
}
//
ans[i - k + 1] = maxHeap.peek()[0];
}
return ans;
}
// @formatter:on
|
复杂度#
n-k+1个组,每组元素进行堆化,复杂度O((n-k+1)*logn)。
省略低阶、常数阶,维护统计数据时间复杂度:O(n*logn)。
最差情况下碰到递增序列,堆维护了n容量的数据。空间复杂度O(n)
使用一个单调递减队列维护当前组的值#
队列头部维护大值,尾部维护小值。
由于每一组只需要获取最大值,因此从队头获取数据O(1)。
保持递减单调:
- 遍历到的新元素大于等于队尾小数据,则将队尾小数据出队,新元素候补上位
- 由于窗口只向前滑动,淘汰的小数据在后续也不会用到,因为候补的更大数据一定在新的窗口内
与使用堆的区别:
- 堆如果没碰到更小的数据时,会一直入堆,堆最大情况下可能维护n个数据。对比的基准值是最大堆堆顶元素。
- 单调队列
- 则在每次加入新元素前都会检查队尾最小元素是否是否更小,如果不是,则将队尾元素出队,保证新加入元素排在队列最小队尾位置
- 同时,检查队头大元素是否越界,越界则将大元素出队,所以单调队列最大只维护k个一组的数据容量
- 对比基准值是队头的当前组最大元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
/**
* 单调队列:使用一个递减队列维护当前组的值
* 头部维护大值,尾部维护小值
* 由于每一组只需要获取最大值,因此从队头获取数据O(1)
* <p>
* 保持递减单调:
* - 遍历到的新元素大于等于队尾小数据,则将队尾小数据出队,新元素候补上位
* - 由于窗口只向前滑动,淘汰的小数据在后续也不会用到,因为候补的更大数据一定在新的窗口内
*
* 与使用堆的区别:
* - 堆如果没碰到更小的数据时,会一直入堆,堆最大情况下可能维护n个数据。对比的基准值是最大堆堆顶元素。
* - 单调队列
* - 则在每次加入新元素前都会检查队尾最小元素是否是否更小,如果不是,则将队尾元素出队,保证新加入元素排在队列最小队尾位置
* - 同时,检查队头大元素是否越界,越界则将大元素出队,所以单调队列最大只维护k个一组的数据容量
* <p>
* 复杂度分析:
* 使用了额外的deque维护组内最大数据,空间复杂度为组的长度k,O(k)
* 完整遍历一遍nums数据,每个数据经历一次入队,一次出队(后面候补更大元素把你淘汰掉了!),整体时间复杂度O(n)
*/
public int[] maxSlidingWindowWithMonotoneDeque(int[] nums, int k) {
int n = nums.length;
Deque<Integer> deque = new LinkedList<>();
// 第一组数据入队!
for (int i = 0; i < k; ++i) {
// 新元素更大,旧元素出队,一直出到以新元素为起点
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
// 新元素入队
deque.offerLast(i);
}
// 单调递减队列:保证从 first->last 递减
int[] ans = new int[n - k + 1];
// 第一组k个元素最大,为队列首
ans[0] = nums[deque.peekFirst()];
for (int i = k; i < n; ++i) {
// 新元素更大,,旧元素出队,一直出到以新元素为起点
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
// 新元素入队
deque.offerLast(i);
// 检查队列头是否已经掉出了k区间左边界,出界元素出队
while (deque.peekFirst() <= i - k) {
deque.pollFirst();
}
ans[i - k + 1] = nums[deque.peekFirst()];
}
return ans;
}
|
复杂度#
完整遍历一遍nums数据,每个数据经历一次入队,一次出队(后面候补更大元素把你淘汰掉了!),整体时间复杂度O(n)。
使用了额外的deque维护组内最大数据,空间复杂度为组的长度k,O(k)。
稀疏表#
TBD
Ref#
