LeetCode 240. 搜索二维矩阵 II 二分变体题解，重新理解二分、BST、局部有序。

题目

240. 搜索二维矩阵 II

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。 每列的元素从上到下升序排列。

思路

看到数组搜索，立马想到了二分，但是最开始我做了一些失败的尝试，我的思路是通过二分定位到最中间的位置，但是挪动边界需要类似DFS的多区域尝试，编码复杂而且性能不佳，遂放弃这个思路。

于是我实现了按行二分的代码，逻辑简单，复杂度O(n*log(m))。但是按行依旧是遍历，同时没有充分利用题干条件：行数据从左到右升序、列数据从上到下升序。

思路启发，还是看了Krahets K神的题解，让我思考：如何在未来碰到类似题目能够有正确思路？

  1. 碰到部分有序的数据时，应该要有一些敏感度，比如BST就是典型的部分有序结构，遍历跳转，其实核心思想与二分是一致的，二分适用于完全有序的数据集，而BST适用于部分有序的数据集；
  2. 对完全无序的数据排序时，逐步部分有序化也是一种正确的思路，比如插入排序 -> 希尔排序；

暴力解

思路

粗暴地对二维数组遍历。这种思路可行，但是不合题意，因为低效。

复杂度分析

时间

O(n*m)时间复杂度。

空间

空间复杂度O(1)。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

public boolean searchMatrixBruteForce(int[][] matrix, int target) {
    int m = matrix[0].length;
    for (int[] ints : matrix) {
        for (int j = 0; j < m; j++) {
            if (ints[j] == target) {
                return true;
            }
        }
    }
    return false;
}

按行二分

思路

二分可以提高行搜索的性能。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

public boolean searchMatrixWithRowBSearch(int[][] matrix, int target) {
    int n = matrix.length;
    int m = matrix[0].length;

    if (target < matrix[0][0] || target > matrix[n - 1][m - 1]) {
        return false;
    }

    int mid;
    for (int[] row : matrix) {
        int low = 0;
        int high = m - 1;
        while (low <= high) {
            mid = low + ((high - low) >> 1);
            if (row[mid] == target) {
                return true;
            } else if (row[mid] < target) {
                low = mid + 1;
            } else if (row[mid] > target) {
                high = mid - 1;
            }
        }
    }
    return false;
}

复杂度分析

时间

时间复杂度O(n*log(m))。

空间

空间复杂度O(1)。

树形二分

思路

借用K神的图，一图醍醐灌顶。

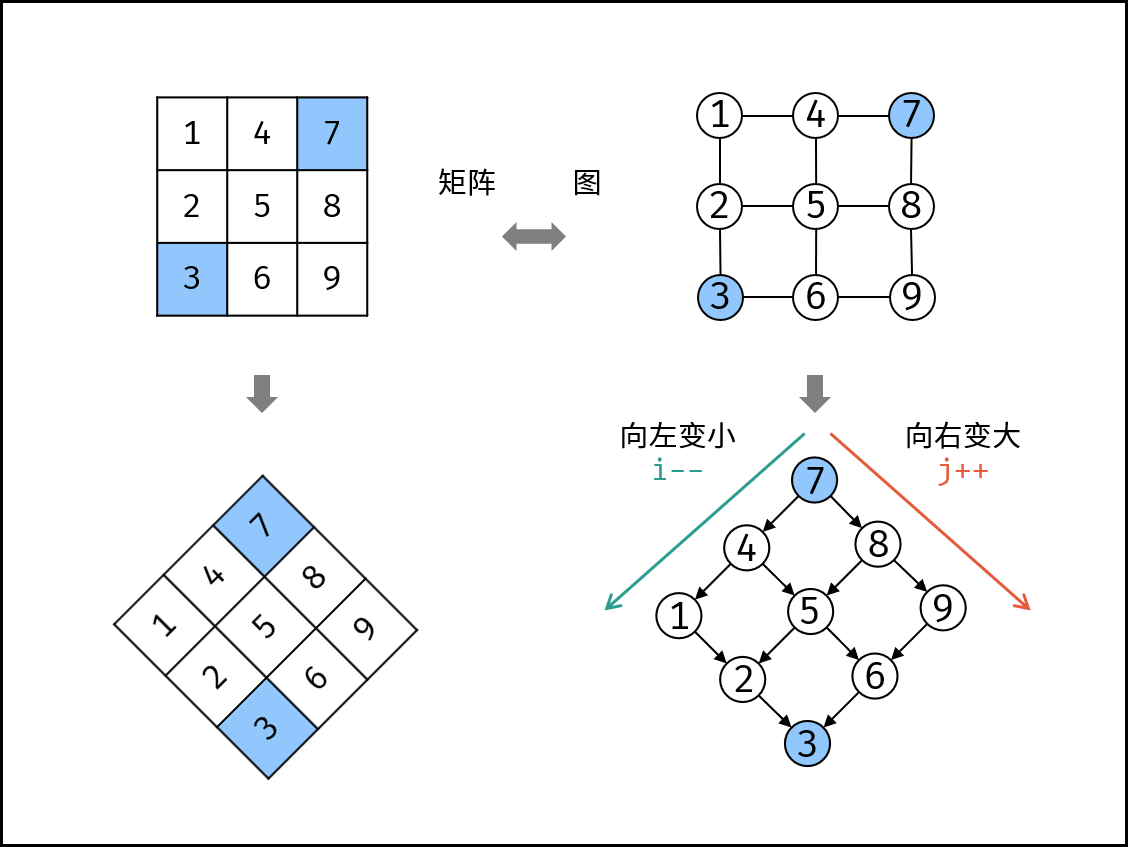
从右上角开始遍历查找，充分利用了题干条件，由于数据已经部分有序，所以其实已经在数据层面做好了二分。

本题中右上角为当前行值最大、列值最小。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

public boolean searchMatrixWithBSearch(int[][] matrix, int target) {
    int n = matrix.length;
    int m = matrix[0].length;

    int x = 0;
    int y = m - 1;

    while (x < n && y >= 0) {
        if (matrix[x][y] == target) {
            return true;
        } else if (matrix[x][y] > target) {
            --y;
        } else {
            ++x;
        }
    }
    return false;

}

复杂度分析

时间

时间复杂度O(n+m)。

空间

空间复杂度O(1)。

Ref