LeetCode 303. 区域和检索-数组不可变 前缀和题解,简单题练习前缀和。
303. 区域和检索-数组不可变#
https://leetcode.cn/problems/range-sum-query-immutable/
给定一个整数数组 nums,处理以下类型的多个查询:
计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left <= right
实现 NumArray 类:
- NumArray(int[] nums) 使用数组 nums 初始化对象
- int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ,包含 left 和 right 两点(也就是 nums[left] + nums[left + 1] + … + nums[right] )
前缀和#
前缀和是一种预处理的方案。在求区间和时,我们可以预先计算出[0,end]区间的和,只需一次集合的遍历,后续查询只做简单的数字运算,记得求得中间区间的和。
公式:
1
|
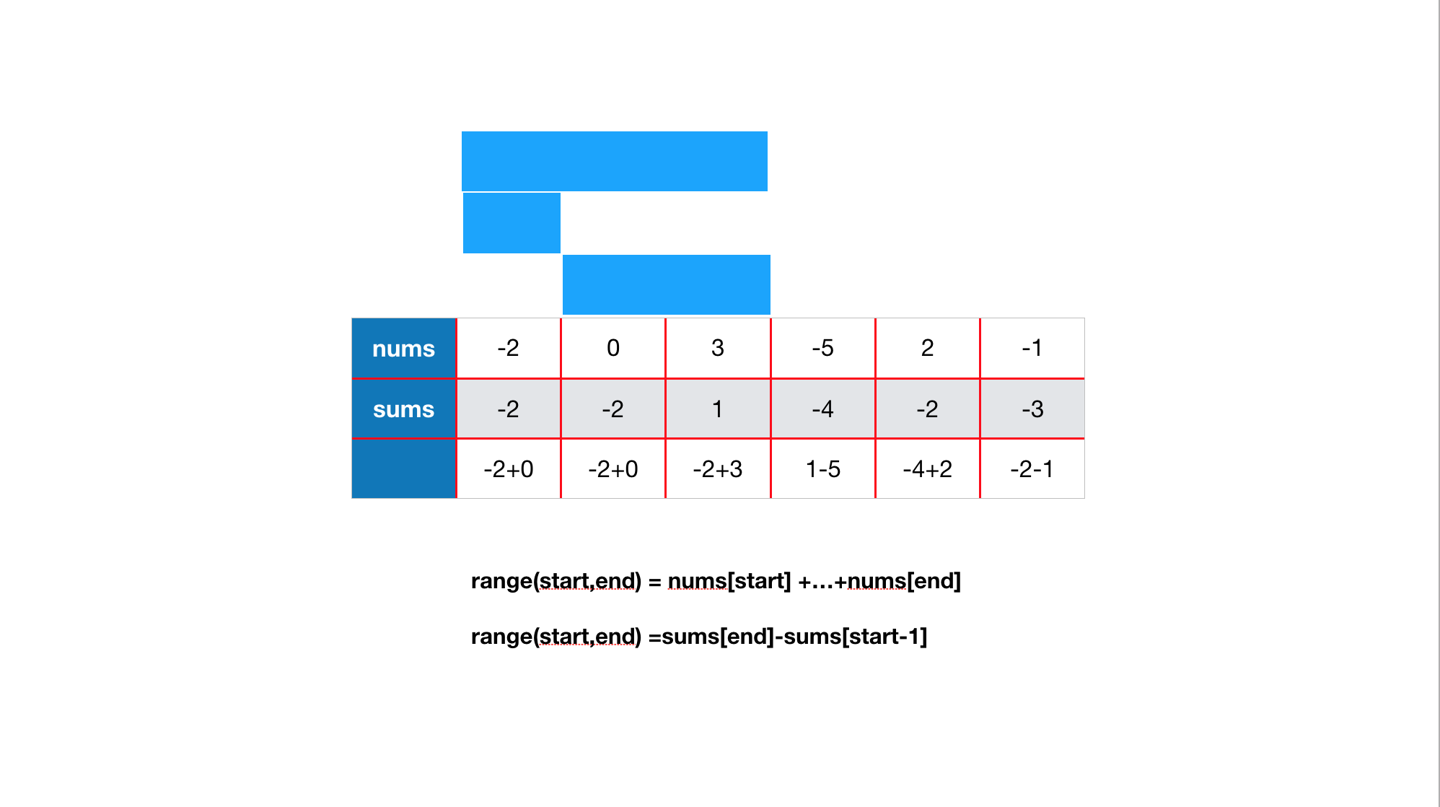
range(start,end) = sum(end) - sum(start-1)
|
如图为这一朴素思路的体现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
public class RangeSumQueryImmutable {
/*
* 执行用时:
* 7 ms
* , 在所有 Java 提交中击败了
* 100.00%
* 的用户
* 内存消耗:
* 44.2 MB
* , 在所有 Java 提交中击败了
* 49.47%
* 的用户
* 通过测试用例:
* 15 / 15
*/
int[] sums;
public RangeSumQueryImmutable(int[] nums) {
this.sums = new int[nums.length];
int preSum = 0;
for (int i = 0; i < nums.length; i++) {
preSum += nums[i];
this.sums[i] = preSum;
}
}
public int sumRange(int left, int right) {
return left == 0 ? sums[right] : sums[right] - sums[left - 1];
}
}
|
复杂度分析#
初始化时需遍历整个入参数组,O(n)时间复杂度。
sumRange()读取时仅需数组寻址读取,O(1)时间复杂度。
sums为额外的数组空间,空间复杂度大致为O(n)。
哨兵写法优化#
上述代码30行,可以看到针对start==0的情况有一个判断处理。
此处可考虑使用 哨兵编程技巧 进行统一化。
如图:
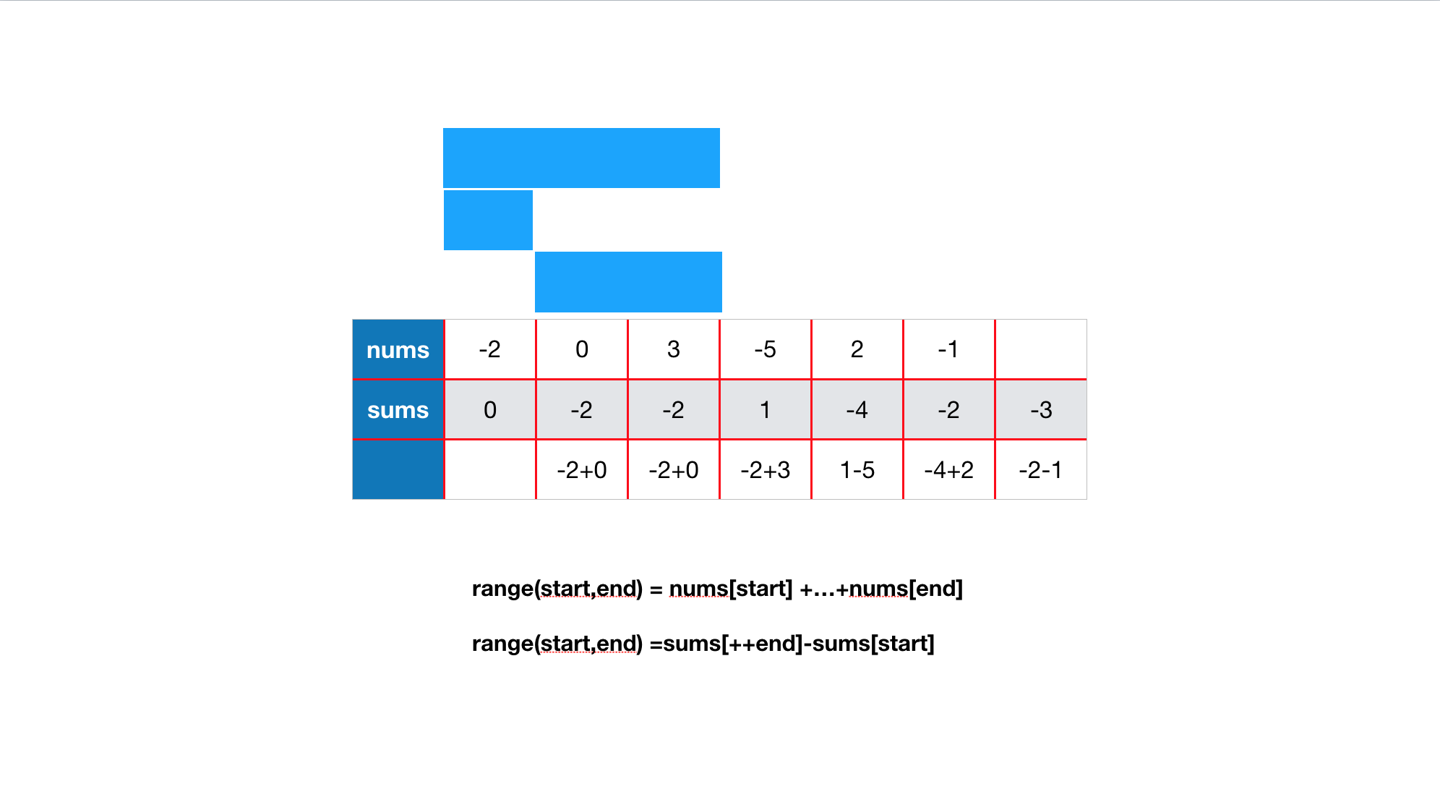
前缀和数组统一右移一位存储、读取。原数组的0位相当于前缀数组的1位,被减项的-1位于前缀树组的合法下标内。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
public class RangeSumQueryImmutableSentinel {
int[] sums;
public RangeSumQueryImmutableSentinel(int[] nums) {
// sums下标统一后移一位,空间 n+1
sums = new int[nums.length + 1];
for (int i = 1; i <= nums.length; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
}
public int sumRange(int left, int right) {
// 读取时下标也右移一位,left++之后,读取的时候也要 left-1,所以不做操作
right++;
return sums[right] - sums[left];
}
}
|
复杂度分析#
同解法1。

