LeetCode 46. 全排列 DFS题解,理解DFS、回溯、递归树。
46. 全排列#
https://leetcode.cn/problems/permutations/
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
全排列这个题目非常适合用来理解回溯、DFS、递归。
官方回溯解#
了解下回溯法的定义:https://suanfa8.com/algorithm-idea/backtracking/01-intro/
回溯完全符合我们自己去思考全排列的过程,比如我们有[1,2,3]:
- 第一步,我们选一个数作为排列中的首项,比如1;
- 第二步,我们选一个数作为第二项,比如2;
- 第三步,我们选一个数作为第三项,此时只剩下3,得到目前的排列[1,2,3];
- 第四步,我们退回第三步,发现选了[1,2]之后没有别的选择,继续回退;
- 第五步,退回到第二步,我们除了2还可以选择3作为第二项,此时2作为第三项,得到新的排列[1,3,2];
- 继续回退到第一步,我们选2作为首项,继续上述过程;
上述过程我们可以用一棵递归树表示,借用官解的图:
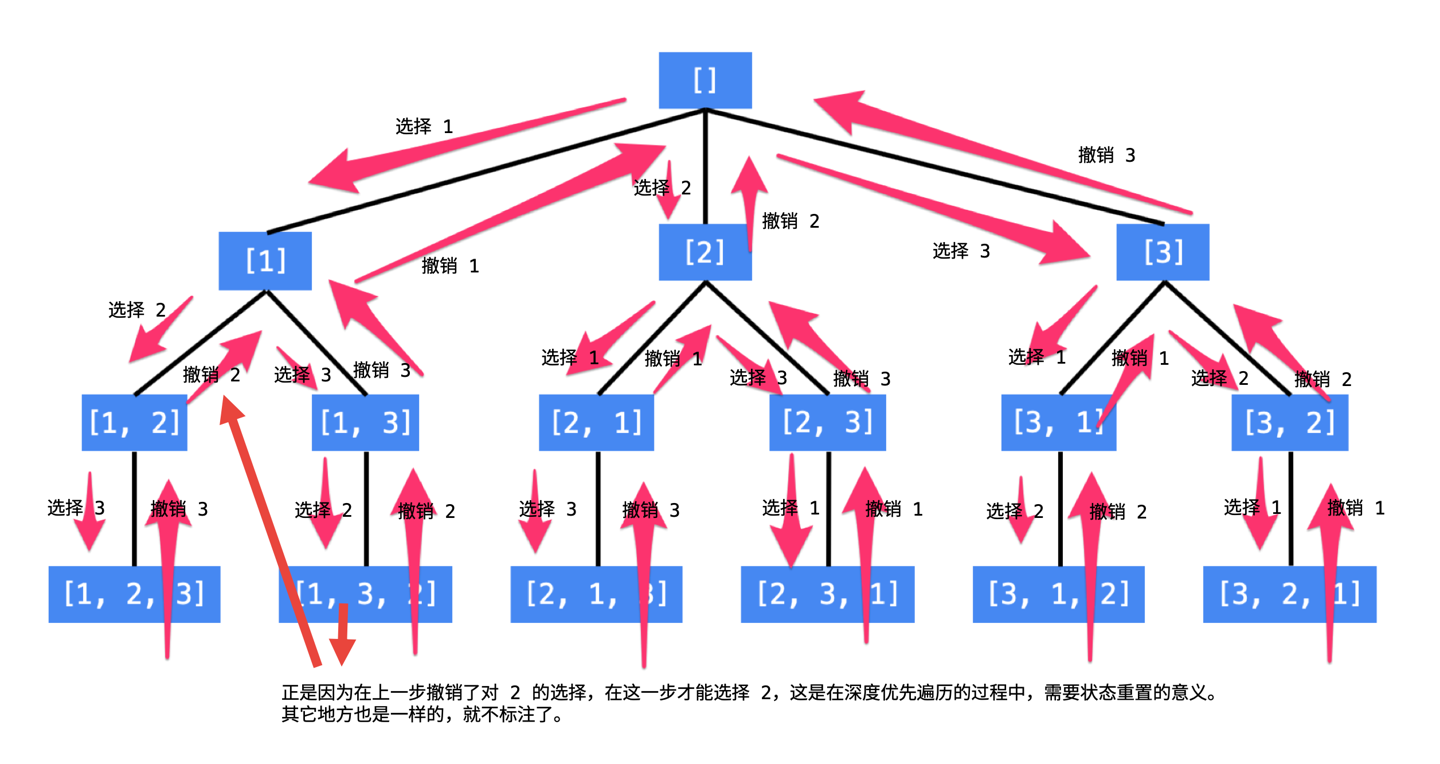
我们简单理解下回溯的框架:
- 题解过程是一棵递归树的执行过程;
- 用
DFS的思路思考,用递归编码;
- 在递归树上遍历路径:
- 寻找解、排除非解(剪枝、
failfast);
- 当前解得出后,树节点回退(撤销状态、状态重置);
- 状态:遍历过程前进后退的进度(对应状态变量、容器);
因此我们的代码有大致框架模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
void dfs(int[] nums, List<Integer> paths, boolean[] usedArr, List<Integer> ansList) {
if (paths.size() == n) {
// 递归对应边界
ansList.add(new ArrayList<>(paths));
return;
}
for (int i = 0; i < nums.length; i++) {
if (usedArr[i]) {
// 判断当前路径下节点遍历状态
continue;
}
usedArr[i] = true;
paths.add(nums[i]);
dfs(nums, paths, usedArr, ansList);
// 回溯:回退之前的状态
usedArr[i] = false;
paths.remove();
}
}
|
回到全排列这道题目,根据以上我们的分析,我们需明确以下几点:
- 使用
DFS递归的形式编码,对应我们的dfs()方法;
DFS遍历,寻找每一种可能的排列,完成一组排列,在递归树上回退状态;- 状态:
- 递归到了哪里?第几层?
- 数组节点值在本轮遍历中是否已被占用?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> ansList = new ArrayList<>();
if (nums == null || nums.length == 0) {
return ansList;
}
int n = nums.length;
// 排列问题,是典型的树形遍历问题,我们使用深度有限遍历的方式走访每个可能的分支
// 使用一个 path 容器,存放当前分支下的数据,回溯即回撤时从末尾回退数据,使用一个栈结构保存
Deque<Integer> pathQueue = new LinkedList<>();
// 同时,我们需要记录每个位置元素使用的状态,为boolean类型数组,同时需要回溯时回退状态
boolean[] usedArr = new boolean[n];
// 深度优先遍历,递归函数
dfs(nums, n, pathQueue, usedArr, ansList);
return ansList;
}
private void dfs(int[] nums, int n, Deque<Integer> pathQueue, boolean[] usedArr, List<List<Integer>> ansList) {
if (pathQueue.size() == n) {
// 递归边界:当分支数据记录到n的数据规模时,递归停止,同时,将记录好的分支数据添加到ansList中
// 如果直接添加pathStack,添加的是引用副本,递归调用中容器内数据会变动,所以我们拷贝一份数据副本
ansList.add(new ArrayList<>(pathQueue));
return;
}
for (int i = 0; i < nums.length; i++) {
if (usedArr[i]) {
// 在当前树路径上该节点已被选
continue;
}
usedArr[i] = true;
pathQueue.offerLast(nums[i]);
dfs(nums, n, pathQueue, usedArr, ansList);
// 回溯:回退之前的状态
usedArr[i] = false;
pathQueue.pollLast();
}
}
|
复杂度分析#
时间复杂度:#
回溯算法时间复杂度复杂度由递归树节点数*节点上的操作决定。
我们假设排列为 A(n,m) 表示从n个数中选m个为一组排列。等同于P(n,m)。
- 非叶子节点数:
- 第一层:A(n,1),从n个数中选一个数;
- 第二层:A(n,2),从n个数中选两个数;
- …
- 倒数第一层:A(n,m-1),从n个数中选m-1 个数;
- 非叶子节点总数为上述和,代入排列公式:
1
2
3
4
5
6
7
|
sum= n!/(n-1)! + n!/(n-2)! + ... + n!/(n-m+1)!
= n!*((1/(n-1)!) + (1/(n-2)!) +...+ (1/(n-m+1)!) )
其中 n==m ,代入公式,得
sum= n!*((1/(n-1)!) + (1/(n-2)!) +...+ 1)
<= n!*((1/(2^(n-1))) + ... + (1/4) + (1/2) +1)
<= n!*2*((2^n-1)/2^n)
< 2n!
|
- 非叶子节点上的操作
- 在每个非叶子节点上我们都通过
dfs()方法去遍历nums,也就是一个节点上我们都得循环查找未使用的位置。这个操作代价为 n(需要给pathQueue装满数据,也就是size==n)。
-
综上,回溯非叶子节点的复杂度为 O(n*2n!)
-
叶子节点数:n!
-
叶子节点上的操作:ansList.add(new ArrayList<>(pathQueue)); 拷贝n个数据的数组,代价为n;
-
综上回溯叶子节点的复杂度为 O(n*n!)
-
综上,整个Permutations回溯的时间复杂度为 O(n*n!)。
空间复杂度:#
全排列一共n!种排列形式,其中每一种排列中,我们使用siz==n的容器空间开销,因此空间复杂度为 O(n*n!)
Ref#
