LeetCode 191. 位1的个数,熟悉 & 的用法。
LeetCode 191. 位1的个数#
https://leetcode.cn/problems/number-of-1-bits/
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在上面的 示例 3 中,输入表示有符号整数 -3。
本题需要我们有二进制的思维。输入是二进制,统计逻辑也是二进制。
逐位判断#
1的二进制也就是末尾1,通过& 1<<i即可判断i位是否为1,每次我们将1左移,同时需注意代码中&的结果显示依然是十进制,因此通过&结果是否为0判断。
复杂度分析#
整个过程遍历一遍32个位,O(32)时间复杂度。
没有额外空间开销,空间复杂度O(1)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
/**
* 执行用时:
* 0 ms
* , 在所有 Java 提交中击败了
* 100.00%
* 的用户
* 内存消耗:
* 39.1 MB
* , 在所有 Java 提交中击败了
* 5.15%
* 的用户
* 通过测试用例:
* 601 / 601
*/
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int cnt = 0;
for (int i = 0; i < 32; i++) {
if ((n & (1 << i)) != 0) {
++cnt;
}
}
return cnt;
}
|
挪动n二进制位#
我们也可以挪动n在二进制中的位,每次消掉n的二进制末位,即每次 >>>1 相当于 /2 ,判断末位是否为1即可计数。
复杂度分析#
同上。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
/**
* 执行用时:
* 0 ms
* , 在所有 Java 提交中击败了
* 100.00%
* 的用户
* 内存消耗:
* 38.5 MB
* , 在所有 Java 提交中击败了
* 50.44%
* 的用户
* 通过测试用例:
* 601 / 601
*/
public int hammingWeight2(int n) {
int cnt = 0;
while (n != 0) {
cnt += n & 1;
n >>>= 1;
}
return cnt;
}
|
这种解法思路下,可以尝试n&(n-1)。
想象n在二进制中的体现,这里借用 负雪明烛大佬 的图:
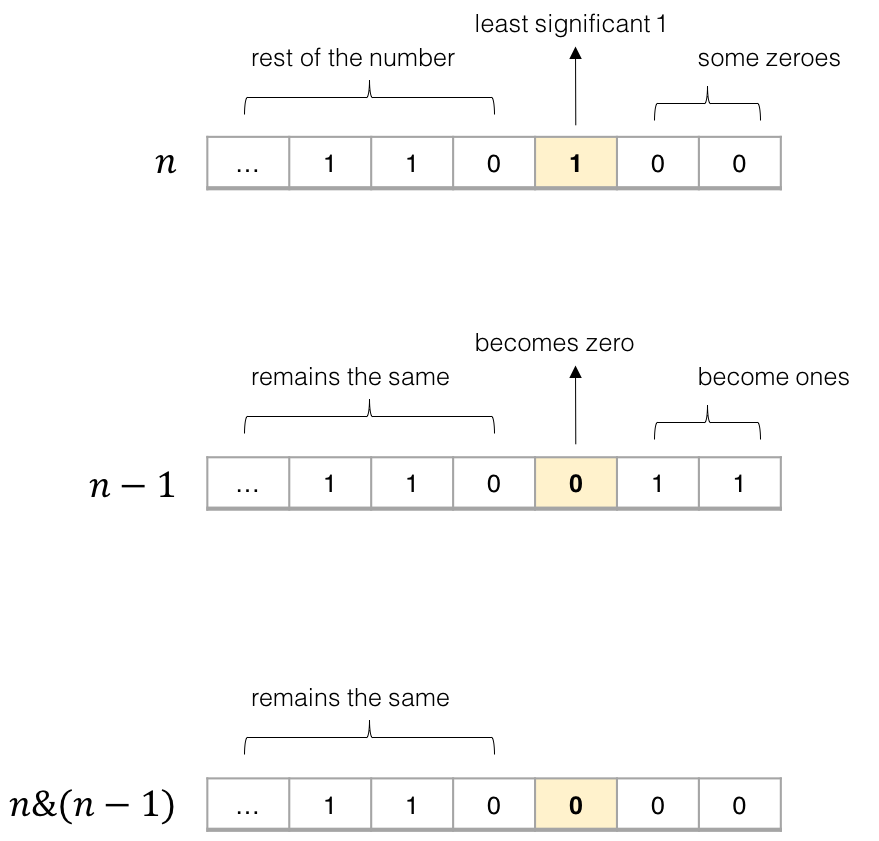
可以看到,n&(n-1)可以将n的末位1消掉,这样挪动比>>>1效率更高、挪动次数更少。
1
2
3
4
5
6
7
8
9
|
public int hammingWeight3(int n) {
int cnt = 0;
while (n != 0) {
++cnt;
// 消除二进制末尾的 1
n &= n - 1;
}
return cnt;
}
|
Ref#
