LeetCode 463. 岛屿的周长 ,熟悉DFS、练习岛屿问题。
463. 岛屿的周长#
https://leetcode.cn/problems/island-perimeter/
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格 子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
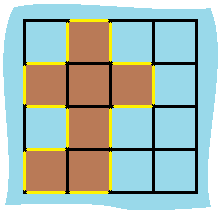
DFS#
DFS核心思想:一杆戳。
对于本题,我们找到第一个陆地节点,然后开始上下左右一顿戳:
- 戳到陆地,说明不是边,周长不动;
- 戳到水,说明是一条边,周长+1;
- 戳出地图边界,说明是一条边,周长+1;
- 同时需要记录访问状态;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
/**
* dfs的思路是:一杆子戳到底,如果戳到了陆地、水区的边界,说明是岛屿的边,那么周长就可以+1
* 同时需要记录访问状态,使用原空间即可,将值标记为666
*/
public int islandPerimeterWithDFS(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
for (int row = 0; row < m; row++) {
for (int col = 0; col < n; col++) {
if (grid[row][col] == 1) {
// 找到了陆地,进入dfs搜索
return dfs(row, col, grid);
}
}
}
return 0;
}
/**
* 执行用时:
* 10 ms
* , 在所有 Java 提交中击败了
* 7.98%
* 的用户
* 内存消耗:
* 42.2 MB
* , 在所有 Java 提交中击败了
* 42.49%
* 的用户
* 通过测试用例:
* 5833 / 5833
*/
private int dfs(int x, int y, int[][] grid) {
int m = grid.length;
int n = grid[0].length;
if (x < 0 || x > m - 1 || y < 0 || y > n - 1 || grid[x][y] == 0) {
// 从陆地来到边界,边长+1
// 从陆地来到水区,边长+1
return 1;
}
if (grid[x][y] == 666) {
// 已访问节点
return 0;
}
// 标记当前点已被访问
grid[x][y] = 666;
int perimeter = 0;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (int[] direction : directions) {
perimeter += dfs(x + direction[0], y + direction[1], grid);
}
return perimeter;
}
|
复杂度分析#
我们发散的时候每次新增四个节点,时间复杂度应该是O(4mn),去掉常数阶O(mn)。
最差情况,矩阵退化成条状,DFS会一杆戳到底,空间复杂度大致为O(mn)。
迭代+数学#
观察题干中给出的图,发现,一个陆地单独出现时,周长为4,一旦与另一个陆地接壤相邻,则周长各自-1,假设有landCnt个陆地,其中有borderCnt个相邻接壤,那么perimeter=4landCnt-2borderCnt。
所以可以尝试迭代遍历的方式,来求解上述中的landCnt/borderCnt。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
/**
* 整个网格被水完全包围,说明我们遍历grid,开始一定是先水,然后才陆地
* 当进入陆地,可以对陆地计数,陆地挨着是陆地,说明 a陆地、b陆地接壤,对周长的贡献分别-1
* 而挨着由于我们已经是遍历过左侧跟上侧,所以检查挨着需要向右、向下
* <p>
* 周长=4*陆地数-2*接壤数
* 对陆地数、接壤数计数即可
*
* @param grid 网格图
*/
public int islandPerimeter(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int landCnt = 0;
int borderCnt = 0;
for (int row = 0; row < m; row++) {
for (int col = 0; col < n; col++) {
if (grid[row][col] == 1) {
landCnt++;
// 向右看相邻
if (col + 1 < n && grid[row][col + 1] == 1) {
borderCnt++;
}
// 向下看相邻
if (row + 1 < m && grid[row + 1][col] == 1) {
borderCnt++;
}
}
}
}
return 4 * landCnt - 2 * borderCnt;
}
|
复杂度分析#
遍历完全整个矩阵,时间复杂度取决于节点个数,为O(mn)。
无额外空间占用,空间复杂度O(1)。
Ref#
