LeetCode 470. 用 Rand7() 实现 Rand10() 进制转换题解,解决一道等概率类型的代表题。
470. 用 Rand7() 实现 Rand10()#
https://leetcode.cn/problems/implement-rand10-using-rand7/
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。
你只能调用 rand7() 且不能调用其他方法。请不要使用系统的 Math.random() 方法。
每个测试用例将有一个内部参数 n,即你实现的函数 rand10() 在测试时将被调用的次数。请注意,这不是传递给 rand10() 的参数。
二进制转换#
由题干可得:rand7 可随机等概率生成 [1,7] 的整数。
求一个可同样等概率生成 [1,10] 整数的函数。
一次调用rand7中,无法生成[8,10]。
尝试多次调用、组合生成的值#
比如,rand7 + rand7,我们看看取值分布:
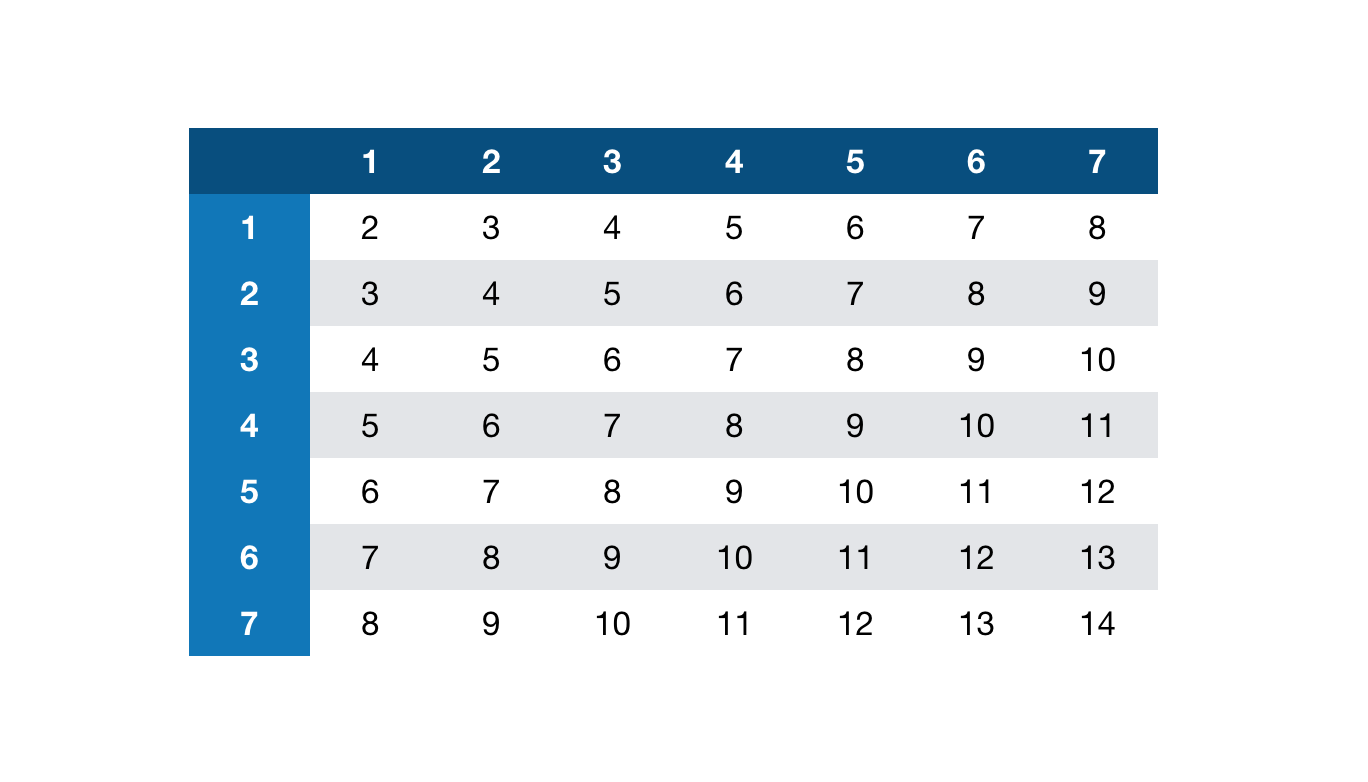
取值并非等概率,并且无法通过分类来区分各个和的含义。
按二进制位生成值#
上面的思路行不通的原因是,求和取值分布不均匀。
我又产生了新的思路:
- 将
rand7改成只生成0/1二进制值的函数;
- 然后组合二进制的 0、1、2、3位,生成一个
[0,2^4]等概率的区间;
- 对二进制转成十进制表示的
[0,2^4] 区间,我们舍弃 [1,10] 区间外的值;
这种组合生成值的方式,由于每次调用生成的值含义不同(位不同),因此值的分布是均匀的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
static class Binary {
/**
* 执行用时:
* 17 ms
* , 在所有 Java 提交中击败了
* 13.32%
* 的用户
* 内存消耗:
* 46.8 MB
* , 在所有 Java 提交中击败了
* 77.39%
* 的用户
* 通过测试用例:
* 12 / 12
*/
public int rand10() {
int ans;
do {
ans = rand16();
} while (ans < 1 || ans > 10);
return ans;
}
public int rand16() {
return (epBaseRand7() << 3) + (epBaseRand7() << 2) + (epBaseRand7() << 1) + epBaseRand7();
}
/**
* 基于rand7实现一个0-1等概率函数
*/
public int epBaseRand7() {
int ans;
do {
ans = rand7();
} while (ans == 4);
return ans < 4 ? 0 : 1;
}
public int rand7() {
return (int) (Math.random() * 7 + 1);
}
}
|
复杂度分析#
期望复杂度为 O(1),最坏情况下为 O(∞)。
无额外空间占用,空间复杂度O(1)。
七进制转换#
在二进制转换中,过程有些绕。
实际上,我们可以直接用rand7 -1 表示七进制生成一位的值。然后使用七进制转成十进制即可,如此一来,只需(rand7() - 1) * 7 + rand7() - 1,rand7单次少调用了一些,代码上也更加简洁。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
/**
* 七进制
*/
static class Septenary {
/**
* 执行用时:
* 18 ms
* , 在所有 Java 提交中击败了
* 10.50%
* 的用户
* 内存消耗:
* 47.2 MB
* , 在所有 Java 提交中击败了
* 15.73%
* 的用户
* 通过测试用例:
* 12 / 12
*/
public int rand7() {
return (int) (Math.random() * 7 + 1);
}
public int rand10() {
int ans;
do {
ans = (rand7() - 1) * 7 + rand7() - 1;
} while (ans < 1 || ans > 10);
return ans;
}
}
|
进阶问题优化#
你能否尽量少调用 rand7() ?
上述我们的实现中,每次rand7()组合调用的值,如果不在[1,10],我们进行了重试,极端情况下,rand7()会调用多次。
实际上,我们可以将组合出来的值进行区间映射:
- 针对二进制转换,我们使用
(epBaseRand7() << 4) + (epBaseRand7() << 3) + (epBaseRand7() << 2) + (epBaseRand7() << 1) + epBaseRand7() 来生成[0,32],其中[0,29] + 1均表示为[1,10]的倍数区间,如此一来,我们只需抛弃等概率分布下的[30,32]取值;
- 针对七进制转换,同样使用
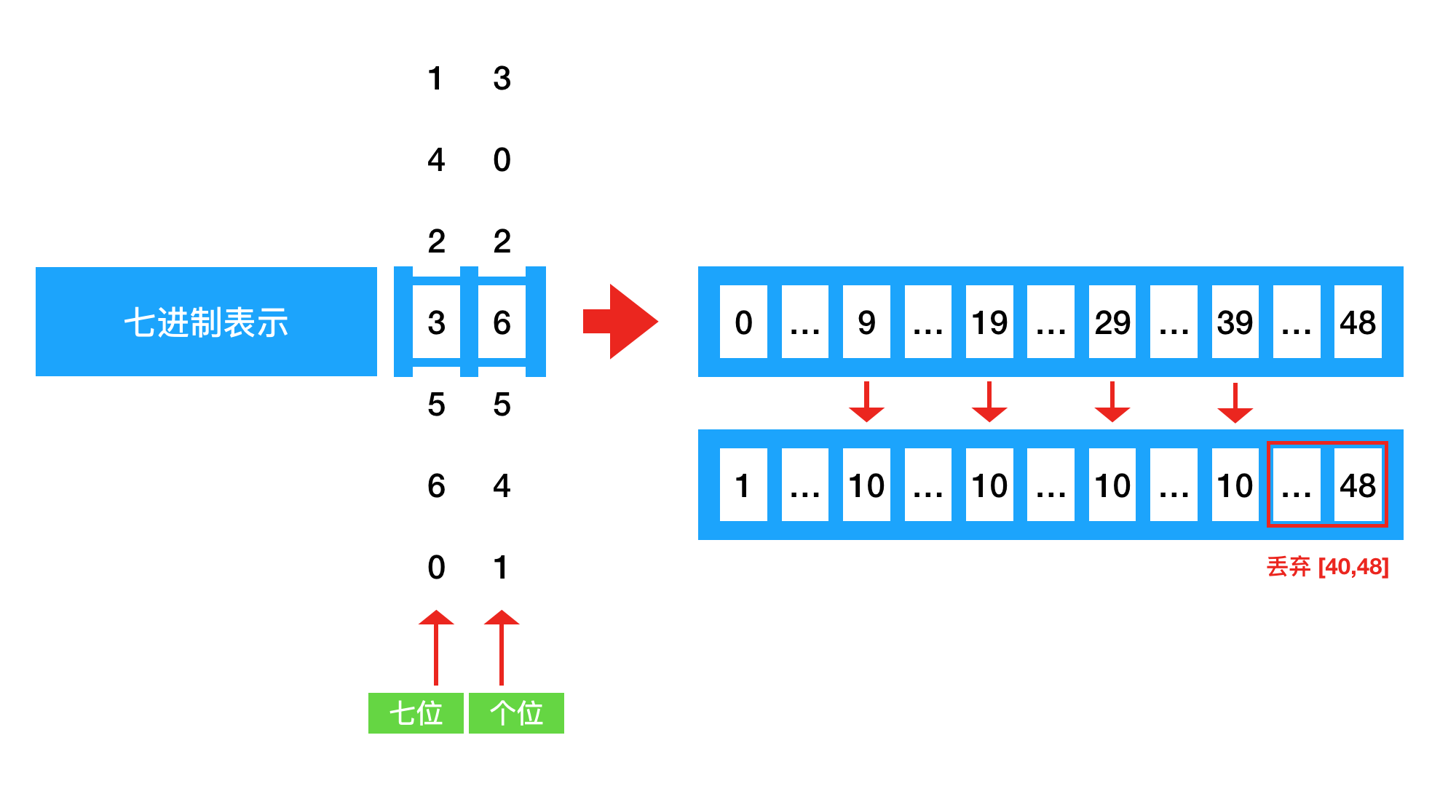
(rand7() - 1) * 7 + rand7() - 1 生成[0,49],其中[0,39] + 1均表示为[1,10]的倍数区间;
通过区间映射,我们可以提高实际运行中生成随机数的利用率。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
/*
* 执行用时:
* 5 ms
* , 在所有 Java 提交中击败了
* 99.37%
* 的用户
* 内存消耗:
* 46.9 MB
* , 在所有 Java 提交中击败了
* 64.81%
* 的用户
* 通过测试用例:
* 12 / 12
*/
/**
* 进阶:将生成的 [11,40] 区间映射到 [1,10],提高随机生成数的利用率
*/
public int rand10Advanced() {
int ans;
do {
ans = (rand7() - 1) * 7 + rand7() - 1;
} while (ans < 1 || ans > 40);
return ans % 10 + 1;
}
|
Ref#

