LeetCode 153. 寻找旋转排序数组中的最小值 二分题解，重新认识二分。

题目

153. 寻找旋转排序数组中的最小值

https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到： 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2] 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7] 注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

思路

这道题与 搜索二维矩阵 II 有一个共同点，那就是数据是保证了部分排序的，结合题干要求复杂度O(log n)，我们可以尝试二分的思路。

二分的核心：每一轮遍历都可以丢弃一些不符合条件的数据，以此提高后续搜索的效率。

  • 朴素二分：针对全局有序的数组，一次丢弃正好一半范围的数据；
  • 树形BST二分：针对排列为树形的数组（二维数组、矩阵），一次可以丢弃一行或者一列的数据；
  • 旋转二分：针对本题这种大小区间不定的情形，一次可以丢弃一半范围的数据；

二分变体解

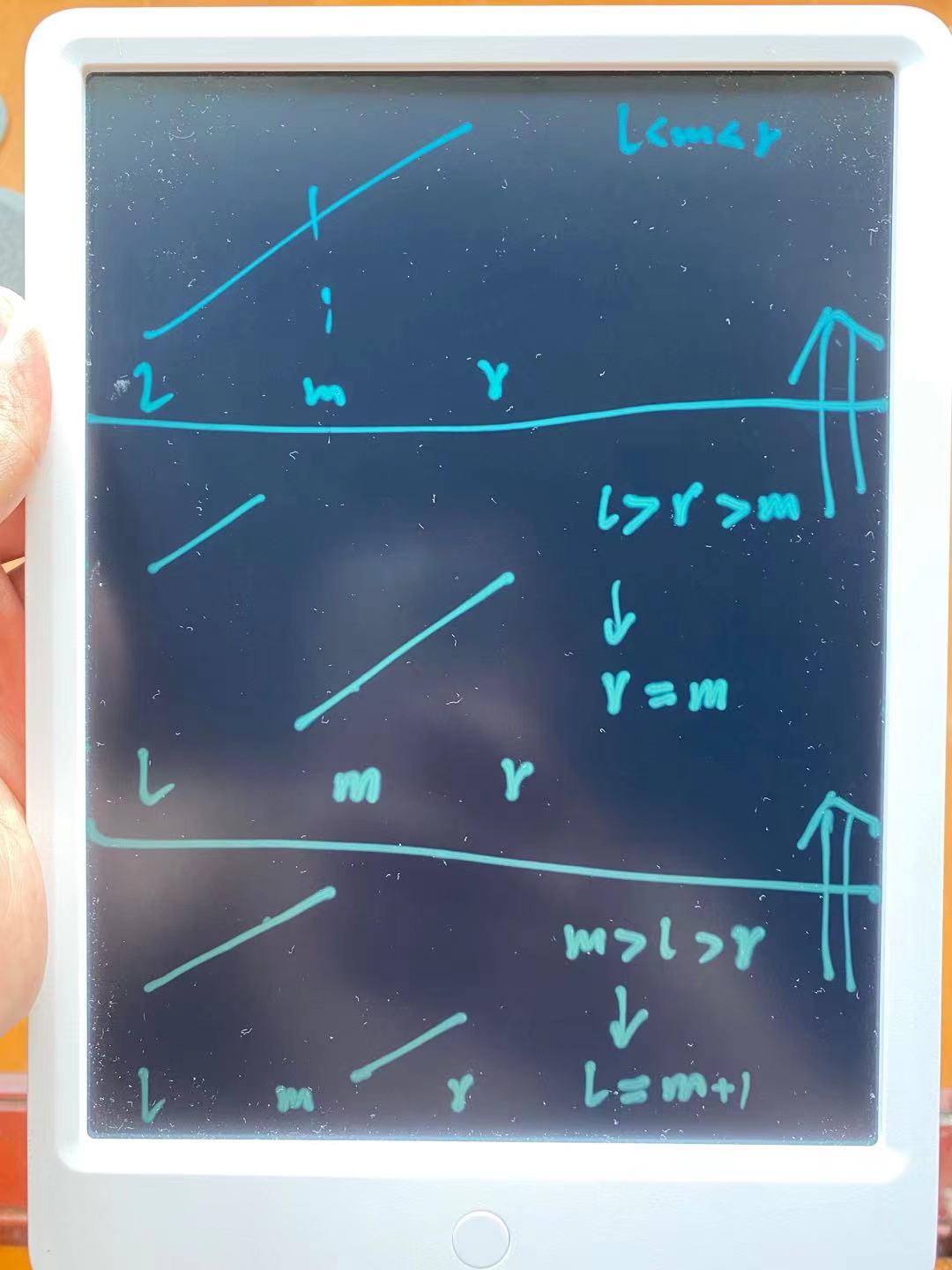
思路

复杂度分析

时间

O(logn)时间复杂度。

空间

无额外空间占用，空间复杂度O(1)。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

/**
    * 执行用时：
    * 0 ms
    * , 在所有 Java 提交中击败了
    * 100.00%
    * 的用户
    * 内存消耗：
    * 40.9 MB
    * , 在所有 Java 提交中击败了
    * 61.54%
    * 的用户
    * 通过测试用例：
    * 150 / 150
    */
public int findMin(int[] nums) {
    int n = nums.length;
    int l = 0, r = n - 1;

    // r不管怎么变，都小于l值
    while (l < r) {
        int mid = l + ((r - l) >> 1);

        if ((nums[l] < nums[mid] && nums[mid] < nums[r]) || (l == mid && nums[l] < nums[r])) {
            break;
        }

        if (nums[r] >= nums[mid]) {
            r = mid;
        } else if (nums[mid] >= nums[l]) {
            l = mid + 1;
        }
    }
    return nums[l];
}

实际上这里代码可以适当简化，只比较右区间值nums[r]与nums[mid]即可判断出上图中的三种情况：

  • nums[r]<nums[mid]：说明mid此时在旋转过的左区间，l向右，l=mid+1；
  • nums[r]>nums[mid]：说明mid在右区间，r向左，r=mid；

只使用nums[l]与nums[mid]比较，上图中的nums[l]<nums[mid]时无法决定挪动左右哪个区间。

简化代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

public int findMin(int[] nums) {
    int n = nums.length;
    int l = 0, r = n - 1;
    while (l < r) {
        int mid = l + ((r - l) >> 1);

        if (nums[r] > nums[mid]) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return nums[l];
}

154. 寻找旋转排序数组中的最小值 II

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到： 若旋转 4 次，则可以得到 [4,5,6,7,0,1,4] 若旋转 7 次，则可以得到 [0,1,4,4,5,6,7] 注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个可能存在 重复 元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中> 的 最小元素 。

二分解

关键需要画图分析用例情况。

思路

154相比153只改变了一个条件：元素可重复。对应循环中的判断新增了一种等值的情况：nums[r] == nums[mid]。

用例分布分析：

  • 无等值元素的情况下，153解法代码即可满足。
  • 有等值元素的情况下
    • 全部等值，不管怎么挪动区间都可以求解
    • 如下图

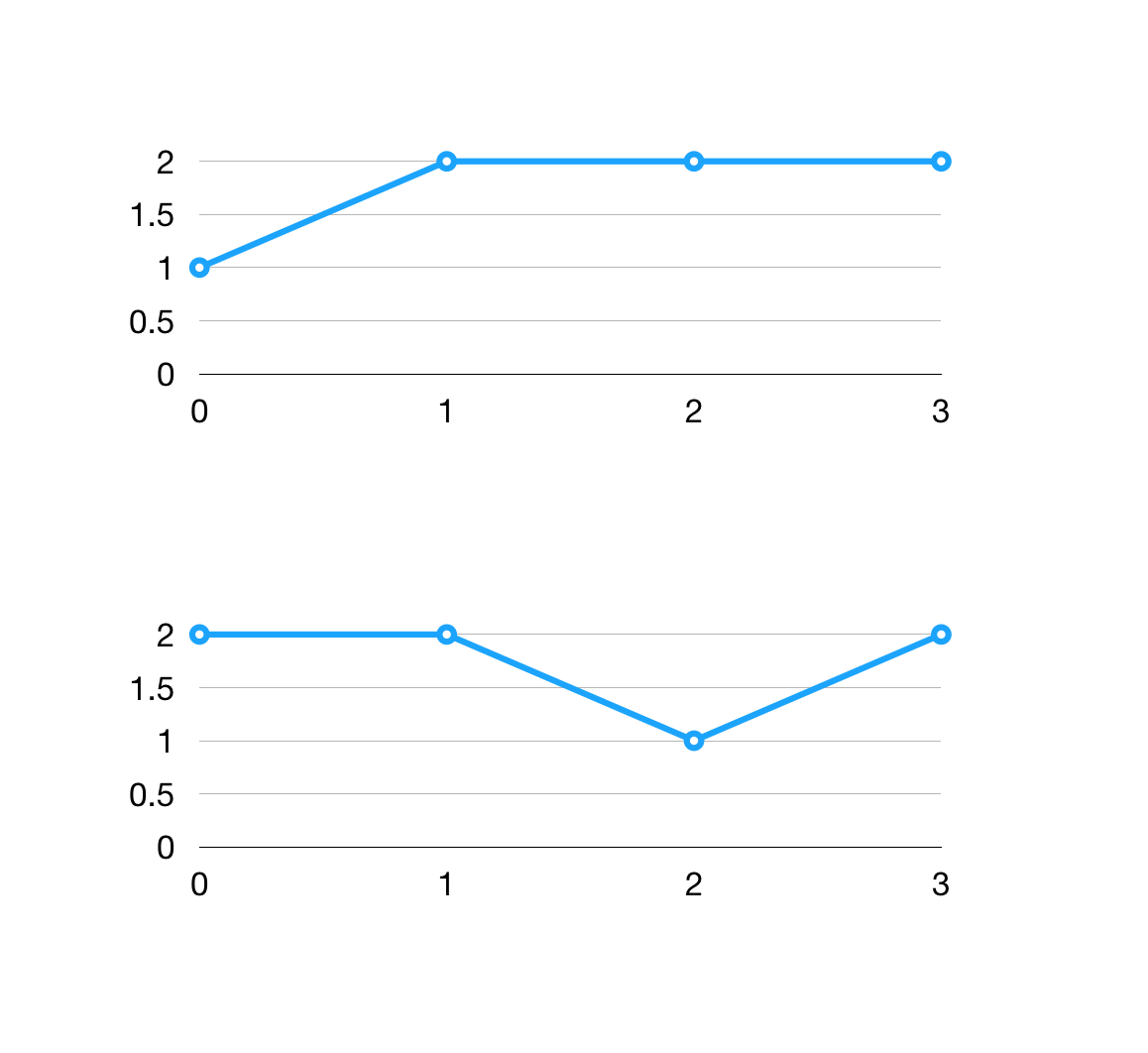
我们再看个用例：[1011111]

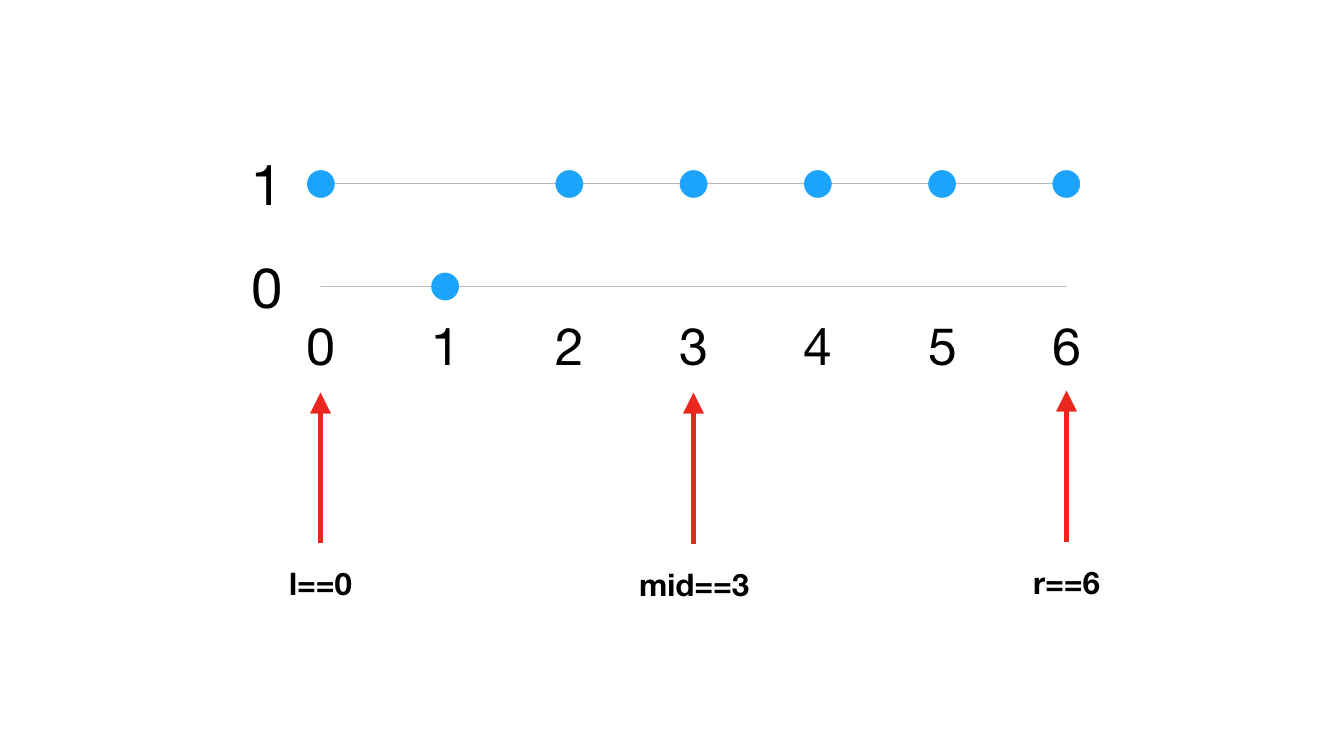
上述两图的情况下，均满足：nums[r] == nums[mid]，这种情况下如果收缩l，上图的第一种情况就会出错，如果收缩r，我们无法直接跳跃到mid的位置，只能逐步收缩，即r=r-1。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

public int minArray(int[] nums) {
    int n = nums.length;
    int l = 0, r = n - 1;

    while (l < r) {
        int mid = l + ((r - l) >> 1);
        if (nums[r] > nums[mid]) {
            r = mid;
        } else if (nums[r] < nums[mid]) {
            l = mid + 1;
        } else {
            r = r - 1;
        }
    }
    return nums[l];
}

Ref