LeetCode 一类题型解析，二分搜索变体：单调序列，单调序列是指非严格递增、非严格递减。

单调序列

概念学习

我们直接看图吧：

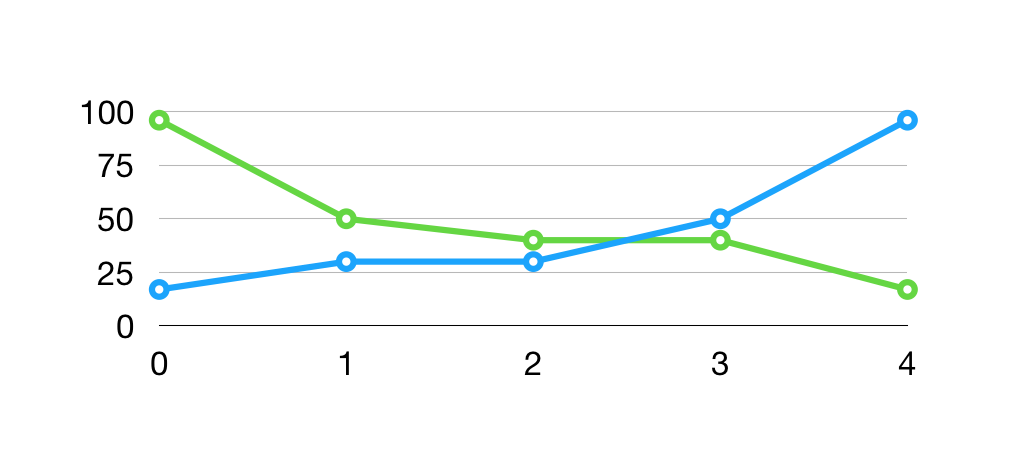
  • 蓝线：表示一个非严格递增序列，其中 blue[1]==blue[2]，由于有等值元素存在，所以非严格递增；
  • 绿线：表示一个非严格递减序列，其中 gree[2]==green[3]，由于有等值元素存在，所以非严格递减；
  • 蓝绿线都是单调序列；

本文通过LC上的实际题目来感受、理解其特征、运用。

二分运用

假设我们处理的序列都是升序的。

朴素二分-找目标值任一位置

朴素二分本质上是通过二分来查找某一个元素的位置，只要找到元素等同于目标值，就可以返回位置。

代码示例：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

    public static int bsearch(int[] nums, int target) {

        int low = 0;
        int high = nums.length - 1;

        while (low <= high) {
            int middle = low + ((high - low) >> 1);
            if (nums[middle] > target) {
                // 重置右边界
                high = middle - 1;
            } else if (nums[middle] < target) {
                // 重置左边界
                low = middle + 1;
            } else {
                return nums[middle];
            }
        }

        // 不存在返回-1
        return -1;
    }

变体-找目标值第一个位置

在朴素类型的基础上，增加一个题干：元素有等值情况，查找元素在序列中的第一个位置。

找最后一个位置是同理的，边界、挪动方向不同而已。

在上述代码基础上，稍做修改：找到等值元素后，我们尝试往左侧挪动，这里增加边界的判断即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

    public static int bsearchFindFirst(int[] nums, int target) {
        int low = 0;
        int high = nums.length - 1;
        while (low <= high) {
            int middle = low + ((high - low) >> 1);
            if (nums[middle] > target) {
                // 挪动右边界
                high = middle - 1;
            } else if (nums[middle] < target) {
                // 挪动左边界
                low = middle + 1;
            } else {
                // 到达左边界 || 左侧的值已经不符合等值条件了  
                if (middle == 0 || nums[middle - 1] < target) {
                    return middle;
                }
                // 往前查找
                high = middle - 1;
            }
        }
        // 不存在目标，返回-1
        return -1;
    }

变体-找大于等于目标值的第一个位置

有序序列中，有可能不存在等值元素，这种时候我们的>=target情况处理就一致了，在上面的代码基础上，我们合并>= if分支。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

    public static int bsearchFindFirstBiggerOrEqual(int[] nums, int target) {
        int low = 0;
        int high = nums.length - 1;
        while (low <= high) {
            int middle = low + ((high - low) >> 1);
            // 合并了 > = 分支
            if (nums[middle] >= target) {
                if (middle == 0 || nums[middle - 1] < target) {
                    return middle;
                }
                high = middle - 1;
            } else if (nums[middle] < target) {
                low = middle + 1;
            }
        }
        // 不存在目标，返回-1
        return -1;
    }

到这里，关于二分的基础做法都覆盖到了。

LC单调序列题目

我们上面有一个假定：题干中直接给出了一个有序序列（大多数时候是一个有序数组）。

而力扣上我们今天要聊的这些题，题干中并没有直接给出这个序列，单调有序序列需要我们根据题干条件自己来写。

我把这类题叫做「生成单调序列」类型题目。

如下是相关题目：

题目 单调序列（y=f(x)）
875. 爱吃香蕉的珂珂 hours=f(speed)：吃得越快，花时间越少。单调递减函数。
1011. 在 D 天内送达包裹的能力 days=f(load)：船的负载能力越大，消耗天数越少。单调递减函数。
1552. 两球之间的磁力 ballsCnt=f(distance)：球与球之间距离越大，能放的球数越少。单调递减函数。
1482. 制作 m 束花所需的最少天数 flowerCnt=f(days)：等越久，成熟的花朵越多。单调递增函数。
LCP 12. 小张刷题计划 days=f(speed)：小张做题越快，花费时间越少。单调递减函数。

可以看到我标出了单调序列，根据题干稍做分析，不难总结出这个单调函数。

下面我们以实际题目为例来做个示范。

题目

153. 寻找旋转排序数组中的最小值

LeetCode 153. 寻找旋转排序数组中的最小值 二分题解

这道题展示的是非单调序列案例，不是本文要看的单调序列，放这里是为了做个对比。

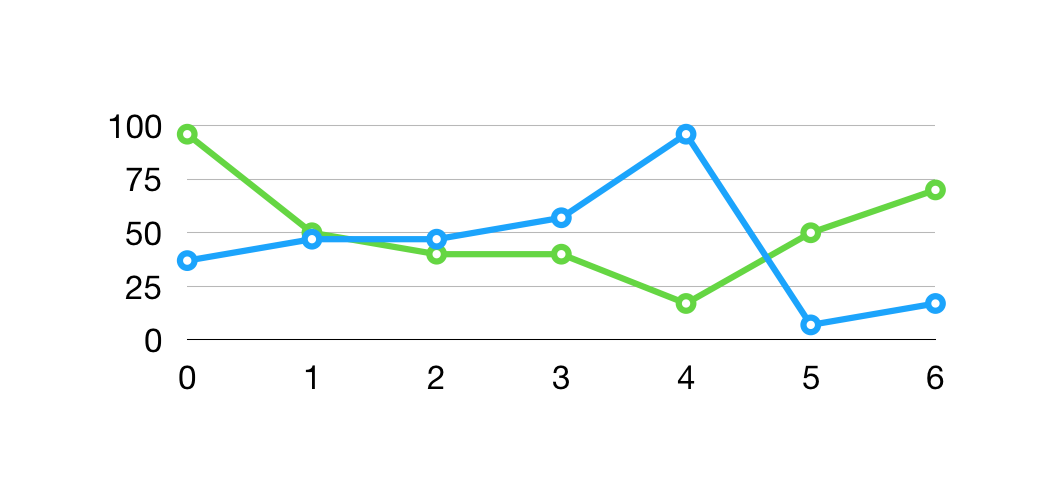
可以看到非单调的序列，会出现 先递增再递减、先递减再递增 的情况。

154题目相比153增加存在等值元素的题干。154符合上图中的蓝线特征。

875. 爱吃香蕉的珂珂

https://leetcode.cn/problems/koko-eating-bananas/

思路

根据上面的分析，我们需要抽象出一个单调函数y=f(x)。

抽象单调函数

一般题目所求就是自变量x，也就是速度，koko吃香蕉的速度决定了吃完的时间，而题目又限定了吃完的时间为h。

因此我们的单调函数表示吃完的时间，自变量为吃香蕉的速度：hours=f(speed)：吃得越快，花时间越少。单调递减函数。

到这一步我们当然可以从最大速度逐个去找，这样复杂度就是O(maxSpeed-minSpeed)。使用二分则可以降低复杂度。

我们每次取当前中间速度，求出对应耗费时间，与h对比，逐步逼近。

题干中还限制koko一次只能吃一堆，因此koko吃香蕉的速度被限制在了[1,max(piles)]，最慢一次吃一根，最快一次把一堆都整完。这样二分的初始边界l r就有了。

函数逻辑

设速度为speed，我们一共有piles个香蕉，依次计算每个香蕉吃几次。piles[i] % speed > 0时，说明当前香蕉需要piles[i] / speed + 1的时间，否则仅需商个时间。

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

    public int minEatingSpeed(int[] piles, int h) {
        // 二分边界，最小速度应该是1，最大速度应该是一堆香蕉的最大值
        int low = 1, high = 0;
        for (int pile : piles) {
            high = Math.max(high, pile);
        }

        // 循环 logm 轮
        while (low <= high) {
            int mid = low + ((high - low) >> 1);
            long hoursNeed = hoursBySpeed(mid, piles);
            if (hoursNeed <= h) {
                // 等值区间是否到达边界
                if (mid == 1 || hoursBySpeed(mid - 1, piles) > h) {
                    return mid;
                }
                // 不是边界，high可以左移
                high = mid - 1;
            } else if (hoursNeed > h) {
                // mid此时不在答案处，low处于非解区间，low可以右移
                low = mid + 1;
            } 
        }
        return -1;
    }

    /**
     * 复杂度 O(n)
     * 速度越大，所需时间越少
     * hoursBySpeed 是一个递减函数
     */
    private long hoursBySpeed(int speed, int[] piles) {
        long hours = 0;
        for (int pile : piles) {
            hours += pile % speed == 0 ? pile / speed : pile / speed + 1;
        }
        return hours;
    }

复杂度分析

时间

设len(piles)=n，每次二分均需求一次n下的速度。

二分整体循环log(max(piles)-1)次。

整体时间复杂度O(len(piles) * log(max(piles)-1))。

空间

空间复杂度O(1)。

小结

碰到这类题，首先我们可以回顾下二分的用法，理解了边界挪动之后，二分就可以作为框架使用。

而针对题干中的单调函数，则需要仔细分析题干，必要时可以画图、分析用例进行逐步推导。