LeetCode 1162. 地图分析,理解BFS+四处发散。
1162. 地图分析#
https://leetcode.cn/problems/as-far-from-land-as-possible/
你现在手里有一份大小为 n x n 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地。
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回 -1。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。
BFS+四处发散#
这个题目是BFS经典题型,属于图计算最短最长路径的概念。这里使用了一个二维数组(矩阵)来表示图。
BFS需要借助一个队列,来维护每层的数据。
由于图有四个方向,因此本题也需要进行四处发散,可以结合代码中的directions数组理解。
相比树的BFS,树是有向的,一次发散只会往下,称为「单源BFS」
而无向图的BFS,一次发散朝多个方向,称为「多源BFS」
同时,我们需要标记已经走过的点。
过程我引用下 sweetiee 的图:
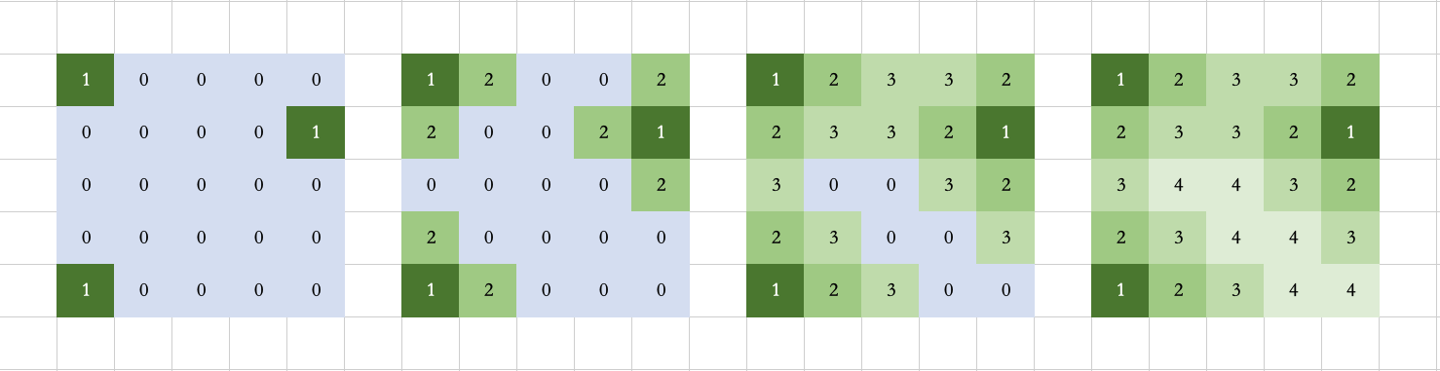
所以过程如同染色:
- 先找到所有的起点(即陆地);
- 通过
BFS+四处发散遍历整个图;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
/**
* 执行用时:
* 12 ms
* , 在所有 Java 提交中击败了
* 87.45%
* 的用户
* 内存消耗:
* 43 MB
* , 在所有 Java 提交中击败了
* 10.63%
* 的用户
* 通过测试用例:
* 37 / 37
*/
public int maxDistance(int[][] grid) {
// n*n 的矩阵
int n = grid.length;
Queue<int[]> pointQ = new LinkedList<>();
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
// 入队所有陆地节点
if (grid[row][col] == 1) {
pointQ.offer(new int[]{row, col});
}
}
}
// 全是海洋或者陆地
if (pointQ.size() == 0 || pointQ.size() == n * n) {
return -1;
}
int[][] directions = {
// 向右,x+1
{1, 0},
// 向左,x-1
{-1, 0},
// 向上,y-1
{0, -1},
// 向下,y+1
{0, 1},};
// bfs 走遍全网格
int[] point = new int[0];
while (!pointQ.isEmpty()) {
int size = pointQ.size();
// 每一层我们同步走完,再走下一层,计算距离可以考虑在层的维度维护一个int,更加直观
for (int level = 0; level < size; level++) {
point = pointQ.poll();
for (int i = 0; i < directions.length; i++) {
int[] direction = directions[i];
int xMove = direction[0];
int yMove = direction[1];
// 越界检查保证了不会出现NPE
int x = point[0] + xMove;
int y = point[1] + yMove;
// 下标不能越界
if (x < 0 || x > n - 1 || y < 0 || y > n - 1
// 0表示海洋,每次访问我们都将海洋点的值更新为距离
|| grid[x][y] != 0) {
continue;
}
// 使用原矩阵,记录点挪动后的距离,因为每次我们只挪动一个单位,所以+1
grid[x][y] = grid[point[0]][point[1]] + 1;
pointQ.offer(new int[]{x, y});
}
}
}
// 我们最开始从1陆地出发,所以计算距离需要减去这个存量1
return grid[point[0]][point[1]] - 1;
}
|
复杂度分析#
n表示矩阵长或者宽。
可以看到我们前序先找陆地节点,会遍历一遍矩阵。
后续从各个陆地节点出发,使用了原数组进行节点访问的标记,保证了每一个节点只访问一次,因此,这里也会遍历一遍矩阵。
时间复杂度为矩阵数据量:O(n^2)。
访问状态没有使用额外空间,而pointQ最多一次可以发散四个节点,不考虑常数阶,空间复杂度O(1)。
Ref#
