从零实现一个最小堆，同时了解堆结构的使用场景。

概念

wiki:

In computer science, a heap is a specialized tree-based data structure which is essentially an almost complete[1] tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C.[2] The node at the “top” of the heap (with no parents) is called the root node.

数据结构中的堆与系统概念中的堆不是一个概念，数据结构的堆是一种逻辑结构，编程语言中的堆往往指一块内存区域、池。

本文以最小堆为例，最小堆是一种基于完全二叉树的数据结构，也叫优先级队列 PriorityQueue，满足以下性质：

  1. 一颗完全二叉树，除了最后一层其它层都满排列，最后一层靠左排列；
  2. 父节点小于等于任一子节点（大顶堆则相反）；

由于完全二叉树向左排列的特性，使用数组存放不浪费空间同时检索高效。

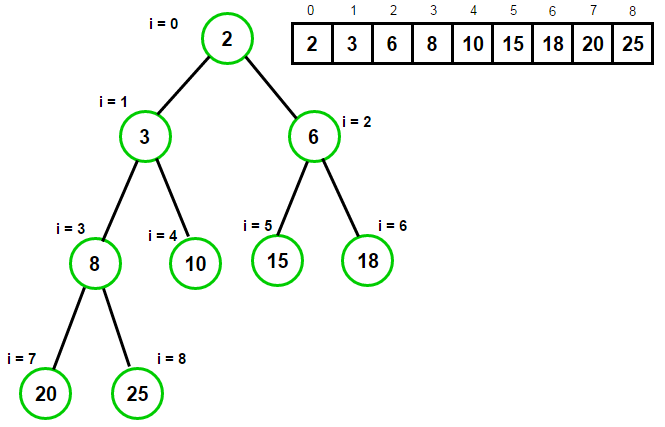
提供的功能包括：

  • 插入新的数据 add
  • 堆化 heapify
    • siftUp 从最小的子节点开始与父节点验证堆性质、合理化
    • siftDown 从最小的父节点开始与子节点验证堆性质、合理化
  • 移除最值 removeMin
  • 查看最值 peekMin

实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

public class MinHeap {

    // 从下标1的位置存完全二叉树堆元素
    int[] arr;
    int capacity;
    int size;

    public MinHeap() {
    }

    public MinHeap(int capacity) {
        this.capacity = capacity;
        arr = new int[capacity + 1];
        size = 0;
    }

    /**
     * 添加元素
     */
    public void add(int ele) {
        if (size == capacity) {
            throw new IllegalStateException("最小堆已满");
        }
        ++size;
        arr[size] = ele;
        siftUp();
    }

    /**
     * 查看最小值（堆顶）元素
     */
    public int peekMin() {
        return arr[1];
    }

    /**
     * 移除最小元素
     */
    public void removeMin() {
        arr[1] = arr[size];
        --size;

        siftDown();
    }

    private void siftDown() {
        // 从顶端开始遍历树，检查堆性质
        int parentIdx = 1;
        int leftChildIdx = getLeftChildIdx(parentIdx);
        int rightChildIdx = getRightChildIdx(parentIdx);
        while (leftChildIdx <= size && rightChildIdx <= size) {
            if (arr[parentIdx] <= arr[leftChildIdx] && arr[parentIdx] <= arr[rightChildIdx]) {
                break;
            }
            int smallerIdx = arr[rightChildIdx] <= arr[leftChildIdx] ? rightChildIdx : leftChildIdx;
            swap(arr, smallerIdx, parentIdx);
            parentIdx = smallerIdx;
            leftChildIdx = getLeftChildIdx(parentIdx);
            rightChildIdx = getRightChildIdx(parentIdx);
        }
    }

    private void siftUp() {
        // 从末端往上检查堆性质
        int childIdx = size;
        int parentIdx = getParentIdx(childIdx);
        while (parentIdx >= 1 && arr[parentIdx] > arr[childIdx]) {
            swap(arr, parentIdx, childIdx);
            childIdx = parentIdx;
            parentIdx = getParentIdx(childIdx);
        }
    }


    public int getParentIdx(int childIdx) {
        return childIdx / 2;
    }

    public int getLeftChildIdx(int parentIdx) {
        return 2 * parentIdx;
    }

    public int getRightChildIdx(int parentIdx) {
        return 2 * parentIdx + 1;
    }
}

关键操作

堆化

堆化是堆结构最核心的方法，本质是逐个节点检验完全二叉树、堆的性质。

sift为筛选的意思

siftUp是从最下的子节点开始逐个节点向上遍历，当前子节点向上与其父节点比较。 可以从上面的代码看到起点是：

1
2

int childIdx = size;
int parentIdx = getParentIdx(childIdx);

而siftDown则是从最下的父节点开始逐个节点向上遍历，当前父节点向下与其子节点比较。 遍历起点是：

1
2
3
4

// 从顶端开始遍历树，检查堆性质
int parentIdx = 1;
int leftChildIdx = getLeftChildIdx(parentIdx);
int rightChildIdx = getRightChildIdx(parentIdx);

建堆

可以考虑两种建堆方式：

  1. 逐个向堆中添加元素； 参考 KthLargestElementInAnArray 中的用例。
  2. 遍历父节点，持续向下siftDown建堆； 参考 HeapSort 中的用例。

复杂度分析

空间

建堆、堆化，是原地操作，无需额外空间，空间复杂度O(1)。

时间

建堆

  • 建堆复杂度取决于树高*节点个数，n个数据树高为 log2n，公式推导:
    • 复杂度= 求和(当前层节点个数 * 当前层高)
    • 设：顶节点高为h，中间层节点数为 2^k，对应中间层高为 h-k，倒数第二层高：1，对应节点数为 2^(h-1)
    • 对复杂度求和：
      • S1 = 2^0 * h + 2^1 * (h-1) + 2^2 * (h-2) + ... + 2^k * (h-k) + ... +2^(h-1) * 1
      • S2 = 2* (2^0 * h + 2^1 * (h-1) + 2^2 * (h-2) + ... + 2^k * (h-k) + ... +2^(h-1) * 1) = 2^1 * h + 2^2 * (h-1) + 2^3 * (h-2) + ... + 2^(k+1) * (h-k) + ... +2^h * 1
      • S2为复杂度*2，S2-S1=S= -h + 2^1 + 2^2 + ... + 2^k + ... + 2^(h-1) + 2^h
      • 代入等比数列去和公式（q公比，S为和，n表示数据量，Sn=(An*q-A1)/(q-1)）
      • 求得 S=-h + (2^h * 2 - 2)/(2 - 1)=-h+2^h
      • 其中 h 为 log2n，所以 S= n -h
    • 因此建堆复杂度为 O(n)，其中h为常数阶省略

堆化

一轮堆化操作复杂度只取决于树高，时间复杂度O(logn)。

性能短板

对数据局部性访问不够友好

堆化父子节点遍历时，会跳跃访问数组元素，以排序为例，快排则是连续访问，因此堆化对CPU缓存行不够友好。

堆排序不稳定

堆化操作会打乱数据原有顺序，还是以排序为例，如果是排序有序度比较高的数据，堆排序先建堆，这一步已经打乱了顺序，后续排序的操作徒增了数组元素交换的次数，而快排、插入排序等算法在这种情况下则不会交换有序元素。

应用场景

排序

用例： https://github.com/redolog/algorithm-java/blob/main/src/test/java/com/algorithm/sort/HeapSortTest.java

堆排序时间复杂度结合上述对堆化复杂度的分析为O(n)，而排序后续元素操作是取出最值元素，将lastChild交换到root的位置继续堆化，持续堆化n-1轮，因此排序复杂度为O(n+n*logn)，去除低阶，得出O(n*logn)。

堆排序在一众排序算法中名列前茅，当然，实际使用需结合上述性能短板的结论。

TopK 问题求解

用例： https://github.com/redolog/algorithm-java/blob/main/src/test/java/com/algorithm/dataStructure/array/KthLargestElementInAnArrayTest.java

使用，假设我们的数据从小到大排列：

  • 最大堆可以维持前k项小数据，堆顶则是这堆小数据中最大的
  • 最小堆可以维持后k项大数据，堆顶则是这堆大数据中最小的

新数据访问时，通过堆顶判断边界，最终堆中维护了整个数据集中的区间最值。

TopK 变体：分位数

如果我们同时持有一个最大堆、一个最小堆，调整两个容器容量比例则可以维持分位值。

比如中位数的比例则是一半一半，元素总数为奇数时，从持有元素个数多一的堆中取堆顶则是中位数。

如果有 n 个数据，n 是偶数，我们从小到大排序，那前 2/n​ 个数据存储在大顶堆中，后 2/n​ 个数据存储在小顶堆中。这样，大顶堆中的堆顶元素就是我们要找的中位数。如果 n 是奇数，情况是类似的，大顶堆就存储 2/n​+1 个数据，小顶堆中就存储 2/n​ 个数据。

实例：

优先级队列

堆本身就是优先级队列。使用这种有序集合我们可以很方便地做一些对顺序有要求的操作：

合并有序文件

假设有十个小的有序文件，如何将里面的数据合并成一个有序文件呢？

我们可以使用堆作为中间容器，每次从十个文件中取最小值放入最小堆，堆中移除堆顶，复杂度仅有O(1)，而如果用数组存放，每次获取要么O(n)，要么每次加入新元素都需要排序，而维持最小堆的有序只需要O(logn)的复杂度。

权重定时器

有序容器中，元素按权重排序。

在定时器场景下，我们的循环每次从队列中取出待执行的定时任务进行对应时段的休眠，一种比较笨的实现思路是每次休眠一秒，拿出任务检查是否到达执行时间，而有了权重后，我们入队时就按照执行时间间隔排好序，出队一个任务按照对应权重休眠对应时间，这样就没有多余损耗。

总结

以上，实现了最基础的一个最小堆最大堆结构，并且分析了复杂度，列举了主流的一些应用场景。

Ref